It is well known that in deep learning the inference phase (inference is defined as the process of deploying a trained model and serving live queries with it) can account up to 90% of the compute costs of the application [1]. This strong energy requirement limits the scalability of the machine learning solution.
In this context, it fits the research of different kind of hardware accelerators that can lower the cost of computation and make the deep learning process more energy efficient [2].
Here, instead, we are going to summarize a novel approach [3] that has been proved of interest and that uses a hybrid architecture made of physical systems to execute the deep learning training and inference phases.
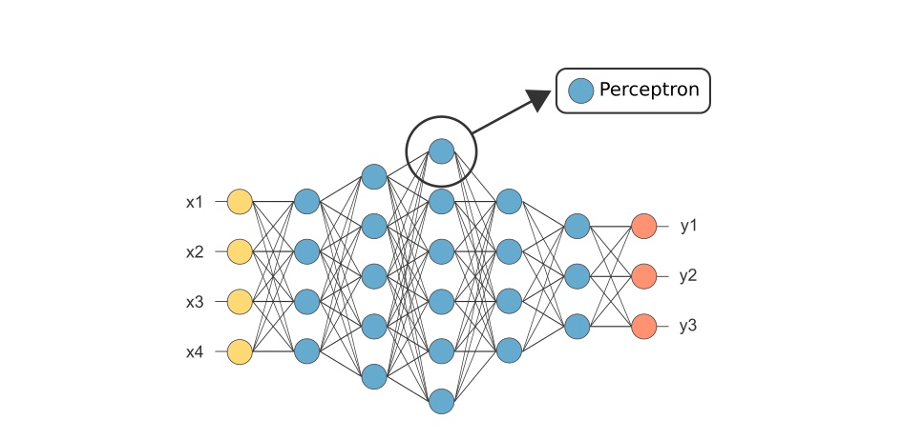
Given the well-known deep neural network (DNN) structure in Figure 1 we have two options to build hardware accelerators:
- Accelerators with the exact mathematical equivalence to the planned neural network that does the exact matrix vector multiplication and applies the same non-linearity as the one in the structure of the figure. This means that you can use a model that has been trained on a GPU, TPU etc. etc. and it is possible to run it on this kind of accelerator perfectly. The downturn of this approach is that the hardware accelerator doesn’t have a good energy efficiency [1]
- Accelerators with approximate mathematical equivalence with the DNN, so that, to inject a model in accelerator like that, we have to re-train it, but with the silver lining to be more energy efficient than the first one.
In this post, we will put attention to an accelerator that falls in the second definition.
The main idea sits behind the following reasoning: In nature, physical system evolution is a kind of computation, so why not try to use a physical system to do the inference calculation for us? This means to turn a given physical system into a neural network.
To understand why this is even possible, let us start describing the inference phase when we want to identify a given digit [4].
The inference phase is the application of an input to the forward neural network, that is composed of different neuron layers, and see how it goes through the network till the output layer. Said that, if we want to recognize a digit, we can encode the digit pixel in the input of the forward network and decode the output once the input propagates through the layer. The main ingredient that allows the propagation of the information is the matrix vector multiplication (parameterize by the weight matrix) and the element-wise non-linearity. As it possible to see in Figure 2, the grey boxes in the lower part of the picture represent matrix vector products done as the input goes through the network.
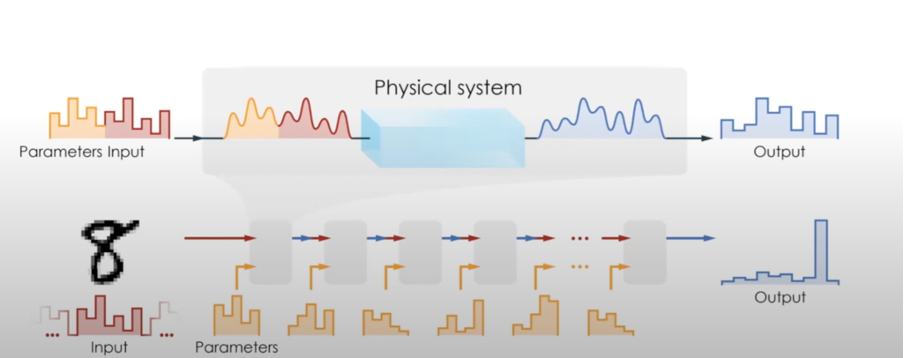
What if we try to substitute what is in the grey boxes with a physical system, feed input data and parameters in it, and let it volve to see the results? Then extract these results and put them in the next grey box, so to construct the different layers of the neural network (NN) as a set of physical systems? (The physical system could be a mechanical resonator, an electronic circuit, etc.)
This is the approach followed by the authors of [3].
They used an optical physical neural network to perform a vowel recognition. It practically consists in feeding to the NN some spoken vowel information and using the system to make a prediction about which vowels were said.
This neural network has five layers as shown in Figure 3.
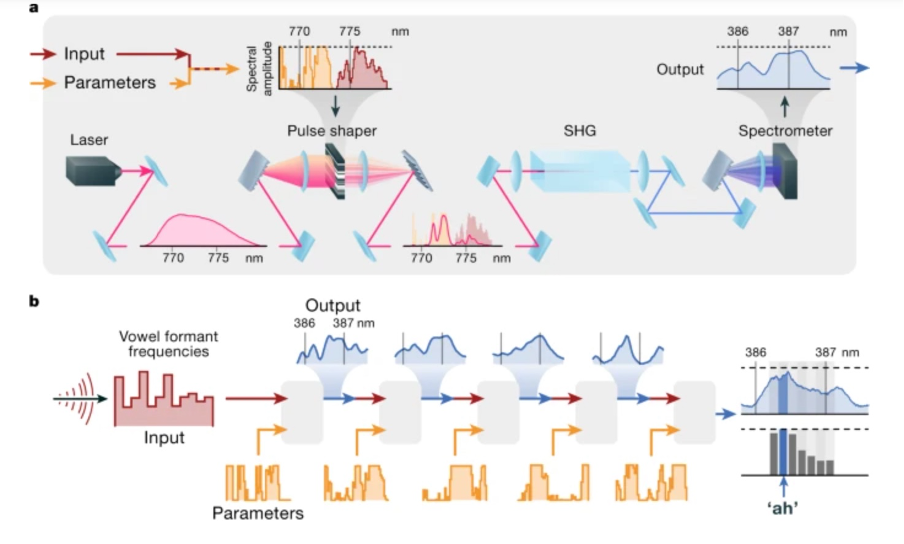
In this Physical Neural Network (PNN) we send the input as a pulse of light that is shaped in its frequency or wavelength domain to encode properly the input data and the parameters. (This phase is done by a pulse shaper that encodes the information about the input data and the parameters.) Then the information flows through a crystal second harmonic generator where a nonlinear optical transformation takes place and, finally, we put it onto a spectrometer to read out the output. The result is then fed into the next layer and so on, like in a standard neural network in which the parameters are different at each layer.
At the end of this phase the training requires a return to the digital world. In fact, in backpropagation we need to run a NN in reverse and this is not possible with physical devices, that do not unmix sounds or other physical “object”.
With this aim, a digital model of each physical system can be built and these models will be reversed on computer so to allow to calculate how to adjust the weights to give accurate answers. This action means that the system is a hybrid architecture half physical and half digital for both training and inference phases.
Practically speaking, the error between the physical system’s output and the desired answer can be exactly computed and back propagated, through the digital model of the physical system that will produce a gradient useful to update the parameters. At the end of this process, it is possible to restart the inference phase cycle, sending new sets of parameters through the physical system again and iterate until needed.
The authors of [3] demonstrated the laser reached 97% accuracy.
The results showed “that not only standard neural networks can be trained through backpropagation but also hybrid system composed of neural network and physical neural network and, given that the physical process has lower energy cost ,we can yield decreasing computational cost, if this technology can be further improved.
So, in general the authors demonstrated that controllable physical systems can be trained to execute DNN calculations and demonstrated that many systems that are not conventionally used for computation appear to offer, in principle, the capacity to perform parts of machine-learning-inference calculations orders of magnitude faster and more energy-efficiently than conventional hardware [3].
References
[2] Reuther, A. et al. Survey of machine learning accelerators. In 2020 IEEE High Performance Extreme Computing Conference (HPEC) 1–12 (IEEE, 2020).
[3] Wright, Logan G., et al. “Deep physical neural networks trained with backpropagation.” Nature 601.7894 (2022): 549-555.
[4] https://medium.com/tebs-lab/how-to-classify-mnist-digits-with-different-neural-network-architectures-39c75a0f03e3
